生日悖论 Birthday Paradox
n 个球投入到 m 个格子中,每个格子都得到少于等于1个球的概率 Pr(C)=i=0∏n−1(1−mi)≈e−mi≈e−n2/2m
当 n=2mlnp1 时,Pr(C)=(1±o(1))p
集合查询问题
问题描述
对于一个包含 n 个元素 x1,x2,…,xn∈U=[n] 的集合 S,查询 x 是否在集合中
Perfect Hashing
完美哈希即不发生冲突,哈希函数 h 是从 [N]→[M] 的所有映射中随机选取的.
Pr(perfect)≈e−n2/2m>1/2,当 m=n2.
Universal Hashing
照搬一下原话
A family H of hash functions in U→[m] is k-universal if for any distinct x1,…,xk∈U,
h∈HPr[h(x1)=⋯=h(xk)]≤mk−11
H is strongly k-universal(k-wise independent) if for any distinct x1,…,xk∈U and any y1,…,yk∈[m]
h∈HPr[i=1⋀kh(xi)=yi]=mk1
生日悖论在两两独立时是 2-universal hashing.
Y=i<j∑I[Xi=Xj], E[Y]≤(rn)m1
FKS Perfect Hashing
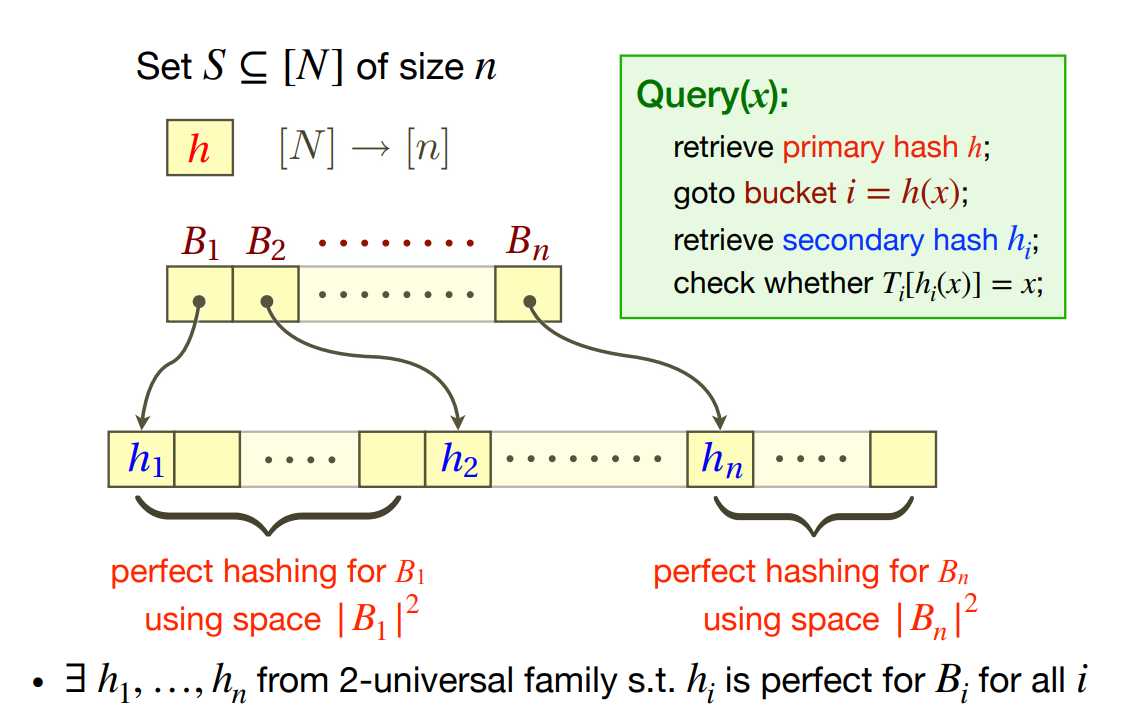
先通过 primary hashing 到 n 个 bucket 中,每个 bucket 再使用 secondary hashing 到对应的位置
对于 n balls into m bins 问题,分析冲突的个数 Y=i>j∑I[Xi=Xj]. 考虑 2-universal 的情况
E[Y]=i<j∑Pr[Xi=Xj]≤(2n)m1
而 Y=i=1∑n(2∣Bi∣)=21i=1∑n∣Bi∣(∣Bi∣−1)
于是有
E[i=1∑n∣Bi∣2]=mn(n−1)+n=O(n)
Approximate set
使用 hash 的方法记录集合中的元素

Bloom Filters
使用多个 hash function hash 到多个位置
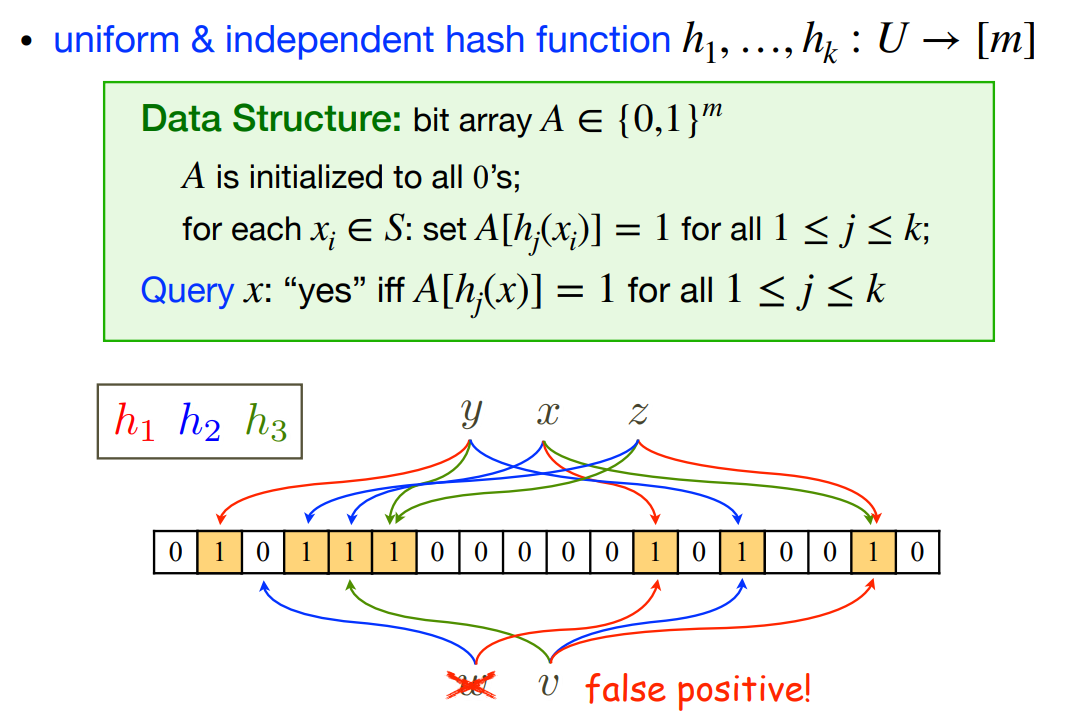
当 s∈/S 时,
===Pr[∀1≤j≤k:A[hj(x)]=1](m#{not empty})k=(m∑I[A[j]=1])k(Pr[A[j]=1])k, w.h.p(1−(1−1/m)kn)k≈(1−e−kn/m)k
元素个数计数
问题描述
给定一串数的序列,估计单独的元素个数 z=∣{x1.x2,…,xn}∣
使用一个均匀分布的哈希函数 h:U→[0,1]. 相当于将 [0,1] 分成 z+1 个区间
E[1≤i≤nminh(xi)]=z+11
所以有估计 Z^=minih(xi)1−1. 令 Y=minih(xi),则有
Pr[Y>y]=(1−y)z p(y)=z(1−y)z−1E[Y2]=∫01y2z(1−y)z−1dy=(z+1)(z+2)2Var[Y]=E[Y2]−E[Y]2=(z+1)2(z+2)z≤(z+1)21
使用多个 hash function 降低方差

此外还有两种估计的方法:Flajolet-Martin Algorithm, BJKST Algorithm


元素频率估计
问题描述
依然是给定一串数,估计某个数出现的频率 fx=∣i:xi=x∣
跟前面的思路一样,利用多个 hash function 得到的值来进行存储






