函数插值

本文关注函数插值的基本知识，包括多项式插值的 Lagrange, Neville, Newton 方法，误差估计，Runge现象，Chebyshev节点，Hermite 插值，三次样条插值

Polynomial Interpolation

---

Problem Setting

本节关注函数插值问题，即给定数据 $(x_1,y_1),\dots,(x_n,y_n),(x_i \neq x_j, \forall i,j)$, 求函数 $f(\cdot)$, 使得 $y_i=f(x_i)$ ，其中 $f(\cdot )$ 要求为 $n-1$ 阶多项式。

Uniqueness

可以证明满足条件的多项式是唯一的。

多项式插值问题可以转化为求解线性方程组。设 $f(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}$

$\begin{bmatrix} 1 & x_1 & \cdots & x_1^{n-1}\\ 1 & x_2 & \cdots & x_2^{n-1}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_n & \cdots & x_n^{n-1} \end{bmatrix} \begin{bmatrix} a_0\\a_1\\ \vdots \\a_{n-1} \end{bmatrix} = \begin{bmatrix} y_1\\y_2\\ \vdots \\y_n \end{bmatrix}$

其系数矩阵为 Vandemonde 行列式，记为 $A$，则有

$det(A)=\prod\limits_{i<j}(x_j-x_i)\not= 0$

所以该线性方程组有唯一解

经过以上的分析，可以知道求解的方法很简单，直接 $A^{-1}y$ 即可求得多项式。但是这样需要对矩阵求逆，计算量很大($O(n^3)$)，所以实际中几乎不可能通过直接求解线性方程组的方法。以下介绍三种多项式插值的方法。

Lagrange’s Approach

Lagrange 多项式插值的中心思想是求一组基 $l_k(x)$，使得

$\begin{cases} l_k(x_i)=1,i = k\\ l_k(x_i)=0,i \not= k \end{cases}$

$l_k$ 的构造基于零点

$l_k(x)=\frac{\tilde p_k(x)}{\tilde p_k(x_k)},\ \tilde p_k(x)=\prod\limits_{i\not= k}(x-x_i)$

对这组基进行线性组合就可以得到满足条件的插值多项式

$f(x)=\sum\limits_{k=1}^ny_kl_k(x)$

实际计算中，构造多项式的系数所需的时间复杂度为 $O(n^2)$，主要在于 $\tilde p_k(x_k)$ 的计算。在计算 $f(x)$ 时，为了减少重复计算，可以先计算 $\prod\limits_{i=1}^{n}(x-x_i)$，再在每一项中除去多余的因数，这样的时间复杂度为 $O(n)$.

Neville’s Approach

Neville 多项式插值的思想是用两个 $n-1$ 个点插值得到的多项式，合成新的由 $n$ 个点插值得到的多项式。

记 $p_1(x)$ 为 $(x_1,y_1),\dots,(x_{n-1},y_{n-1})$ 插值得到的多项式，$p_2(x)$ 为 $(x_2,y_2),\dots,(x_{n},y_{n})$。考虑用这两个多项式的组合得到新的满足条件的多项式 $p(x)$，即

$p(n)=\alpha_1(x-\alpha_2) p_1(x)+ \beta_1(x-\beta_2)p_2(x)$

为了使得 $x_1,x_n$ 满足条件，可以使 $\alpha_2=x_n,\beta_2=x_1$；为了使剩余点满足条件，可以使系数之和为 $1$，即相当于 $p_1,p_2$ 的仿射组合。最终可以得到

$p(x)=\frac{x_n-x}{x_n-x_1}p_1(x)+\frac{x-x_1}{x_n-x_1}p_2(x)$

在插值问题中，通常考虑内插值，即 $x_1\le x\le x_n$，此时 $p(x)$ 相当于做了一个凸组合。

这么做的好处是凸组合具有数值稳定性的。设 $a=\alpha b+(1-\alpha)c$，$b,c$ 的误差分别为 $\delta b,\delta c$，则有

$\delta d\le \alpha\delta b + (1-\alpha) \delta c \le \max(\delta b,\delta c)$

Newton’s Approach

Newton 多项式插值的思想是在前 $n-1$ 个点插值得到的多项式 $p_{n-1}$ 的基础上加上修正，使 $p_n$ 满足条件。由于 $p_{n-1}$ 为 $n-2$ 阶多项式，并且要使前 $n-1$ 个点都满足条件，可以使

$p_n(x)=p_{n-1}(x)+\alpha_{n-1}\prod\limits_{i=1}^{n-1}(x-x_i)$

根据多项式插值的唯一性，$\alpha_{n-1}$ 与 Lagrange 插值的最高次系数应该相等。对比即可知道

$\alpha_{n-1}=\sum\limits_{i-1}^ny_i\prod_{j=1\atop j\not= i}^n(x_i-x_j)^{-1}$

实际上，$\alpha_{n-1}$ 也被称为 $n$ 阶差商 $f[x_1,x_2,\dots,x_n]$

差商具有以下几点性质：

• 递归定义

$\begin{aligned} f[x_k]&=y_k\\ f[x_1,x_2,\dots,x_k]&=\frac{f[x_2,x_3,\dots,x_k]-f[x_1,x_2,\dots,x_{k-2}]}{x_k-x_1} \end{aligned}$

• 对称性：对于任意排列 $\sigma$，有

  $f[x_1,x_2,\dots,x_k]=f[\sigma(x_1),\sigma(x_2),\dots,\sigma(x_k)]$

• 当 $f$ 充分光滑时，有

  $\lim\limits_{(x_1,\dots,x_k)\to (x_*,\dots,x_*)}f[x_1,\dots,x_k]=\frac{f^{(k-1)}(x_*)}{(k-1)!}$

Polynomial Reconstruction

---

Problem setting

本节在上一节问题的基础上加上 $(x_i,y_i)$ 是在函数 $y=f(x),\ x\in[a,b]$ 上采样的点的条件，重点关注重构多项式 $p_{n-1}$ 的效果好坏。

Error Bound

根据牛顿法多项式插值，对于任意点 $x$，有

$\begin{aligned} f(x)-p_{n-1}(x)&=f[x_1,x_2,\dots,x_n,x]\prod\limits_{i=1}^n(x-x_i)\\ &=\frac{f^{(n)}(\xi)}{n!}\prod\limits_{i=1}^n(x-x_i) \end{aligned}$

因此，可以得到以下误差界

$\begin{aligned} |f(x)-p_{n-1}(x)|&\le \frac{\sup\limits_{t\in[a,b]}f^{(n)}(t)}{n!}\prod\limits_{i=1}^n(x-x_i)\\ \left\|f(x)-p_{n-1}(x)\right\|_{\infty}&\le \frac{\|f^{(n)}(x)\|_{\infty}}{n!}\left\|\prod\limits_{i=1}^n(x-x_i)\right\|_\infty \end{aligned}$

可以看到误差界由两部分组成：前一项由函数的性质决定，这是多项式重构中不可避免的一项；而后一项与采样的点有关，采样地越好，误差就会越小。

Runge’s Phenomenon

由于函数 $f$ 本身的性质而导致重构误差大的现象被称为龙格现象，它的数学表示为

$\limsup_{n\to\infty}\|f(x)-p_n(x)\|_\infty>0$

典型的例子有 $f(x)=(1+x)^{-1}$.

Chebyshev Nodes

为了减小多项式重构的误差，需要寻找合适的采样点来最小化 $\left\| \prod\limits_{i=1}^n(x-x_i)\right\| _\infty$

首先考虑 $[a,b]=[-1,1]$ 的情况。事实上，最优的采样点为 Chebyshev 结点，即

$x_i=\cos\frac{(2i-1)\pi}{2n},i\in \{1,2,\dots,n\}$

令 $T_n(x)=2^{n-1}\prod\limits_{i=1}^n(x-x_i)$，对比函数的根和首项系数并根据插值多项式的唯一性，可以得到

$T_n=\cos(n\arccos x)$

即为 Chebyshev 多项式。很显然 $\|{T_n(x)}\|_\infty\le1$，所以有 $\min\left\|\prod\limits_{i=1}^n(x-x_i)\right\|_\infty\le\frac{1}{2^{n-1}}$.

接下来只需要证明 $\min\left\|\prod\limits_{i=1}^n(x-x_i)\right\|_\infty=\frac{1}{2^{n-1}}$。假设存在首一多项式 $f,\ \deg f=n-1$，使得 $\left\|f\right\|_\infty<\frac1{2^{n-1}}$

令 $g(x)=2^{n-1}f(x)-T_n(x)$，那么 $\deg g\le n-1$。

考虑点 $z_i=\cos\frac{i\pi}{n},\ i \in \{0,1,\dots,n\}$，有

$g(z_i)=2^{n-1}f(z_i)-(-1)^i$

由于 $\left\|2^{n-1}f\right\|_\infty<1$，所以 $g(z_i)$ 的符号完全由后一项决定。根据零点存在性定理，$g(x)$ 有 $n$ 个点，这与 $\deg g \le n-1$ 矛盾。所以有最佳采样点为 Chebyshev 结点。利用仿射变换即可以推广到任意区间 $[a,b]$ 上去，可以得到

$x_k=\frac{a+b}2+\frac{b-a}2\cos\frac{(2k-1)\pi}{2n}$

误差界为

$\left\|f(x)-p_{n-1}(x)\right\|_\infty\le \frac{\left\|f^{(n)}(x)\right\|_\infty}{2^{n-1}n!}\left(\frac{b-a}2\right)^n$

Hermite Interpolation

---

Problem Setting

在这里不仅要求采样函数值满足条件，还要求在这些点处的导数满足要求，即

$\begin{matrix} p(x_1)=f(x_1) & p'(x_1)=f'(x_1) & \cdots & p^{(m_1)}(x_1)=f^{(m_1)}(x_1)\\ p(x_2)=f(x_2) & p'(x_2)=f'(x_2) & \cdots & p^{(m_2)}(x_2)=f^{(m_2)}(x_2)\\ \vdots & \vdots & \vdots & \vdots\\ p(x_n)=f(x_n) & p'(x_n)=f'(x_n) & \cdots & p^{(m_n)}(x_n)=f^{(m_n)}(x_n) \end{matrix}$

其中 $m$ 不要求相等.

Solution

实际上，这个问题可以转化为允许重结点的 Newton 插值，将 $x_i$ 看作 $m_i$ 个 $x_i$ 作插值，差商可以看作导数，即

$f[x_i,x_i]=\frac{f'(x_i)}{1!},\ \ \ f[x_i,x_i,x_i]=\frac{f''(x_i)}{2!},\ \ \ \dots$

Matrix Function

Hermite 插值与矩阵函数非常相关。

根据 Cayley-Hamilton 定理，$A^n$ 可以被 $I,A,\dots,A^{n-1}$ 线性表示。因此对于任意矩阵函数 $f(A)$，进行 Taylor 展开后可以表示为一个 $n-1$ 阶多项式，$f(A)=p(A)$.

根据 Jordan 标准型，求 $f(A)$ 等价于求 $f(J)$. 而对于一个 Jordan 块 $J_k$，形如

$J_k= \begin{bmatrix} \lambda_k & 1 & & & \\ & \lambda_k & 1 & & \\ & & \ddots & \ddots & \\ & & & \lambda_k & 1 \end{bmatrix}$

根据 Taylor 展开，有

$f(J_k)=\begin{bmatrix} f(\lambda_k) & \frac{f'(\lambda_k)}{1!} & \frac{f''(\lambda_k)}{2!}&\cdots\\ & f(\lambda_k) & \frac{f'(\lambda_k)}{1!} & \cdots\\ & & f(\lambda_k) & \cdots\\ & & & \cdots \end{bmatrix}$

因此，求矩阵函数相当于对 $\lambda_1,\dots,\lambda_k$ 做 Hermite 插值.

Spline Interpolation

---

样条函数即分段多项式.

Linear Spline

线性样条是最简单的样条插值，它相当于用直线将相邻插值点相连。

假设插值点为 $x_0<x_1<\cdots<x_n$，且 $h_i=x_{i+1},\ h=\max h_i$. 那么在区间 $[x_i,x_{i+1}]$ 上，线性样条为

$s_i(x)=f(x_i)+\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}(x-x_i)$

线性样条虽然简单，但它也有很好的性质：不会产生不必要的震荡。它的问题在于在插值点处不可导，光滑性不好。

接下来进行误差分析。线性样条在一个区间上相当于 $n=2$ 时的多项式插值，根据上面的结论，有

$\left\|s(x)-f(x)\right\|_\infty\le\frac{\left\|f''(x)\right\|_\infty}2 |(x-x_i)(x-x_{i+1})|\le\frac{\left\|f''(x)\right\|_\infty}8h^2$

Cubic Hermite

对于每个区间 $[x_i,x_{i+1}]$，使用三次函数 $s_i(x)=a_ix^3+b_ix^2+c_ix+d_i$ 进行插值，其中 $s_i$ 满足

$\begin{matrix} s_i(x_i)=f(x_i) & s_i(x_{i+1})=f(x_{i+1})\\ s_i'(x_i)=f'(x_i) & s_i'(x_{i+1})=f'(x_{i+1}) \end{matrix}$

这样的好处是导数连续，问题也显而易见，需要各插值点的导数。

Cubic Spline

与 三次 Hermite 插值一样，采用三次样条 $s_i$ 进行插值，其中 $s_i$ 满足

$\begin{aligned} & s_i(x_i)=f(x_i),\ s_i(x_{i+1})=f(x_{i+1})\\ & s'_i(x_{i+1})=s'_{i+1}(x_{i+1})\\ & s''_i(x_{i+1})=s''_{i+1}(x_{i+1}) \end{aligned}$

这样能保证二阶导数连续，并且只需要函数值。

参数有 $4n$ 个，但是上述约束只有 $4n-2$ 个，所以需要增加另外的要求，通常是对端点 $x_0,x_n$ 增加条件。

• Complete 完全样条

  $s'_0(x_0)=k_0,\ s'_{n-1}(x_n)=k_n$

• Natural 自然样条

  $s''_0(x_0)=s''_{n-1}(x_n)=0$

• Periodic 周期样条，要求 $f(x_0)=f(x_n)$

  $s'_0(x_0)=s'_{n-1}(x_n),\ s''_0(x_0)=s''_{n-1}(x_n)$

• Not-a-knot

  $s'''_0(x_1)=s'''_{1}(x_1),\ s'''_{n-2}(x_{n-1})=s'''_{n-1}(x_{n-1})$

三次样条的求解可以使用与 Lagrange 插值相同的思路，先找出基函数，再进行线性组合。

令 $y_i=f(x_i),\ \phi(x)=3x^2-2x^3,\ \psi(x)=x^3-x^2$，设 $k_i=f'(x_i)$，那么可以求得，满足函数值和一阶条件的样条为

$s_i(x)=y_i\phi\left(\frac{x_{i+1}-x}{h_i}\right)+y_{i+1}\phi\left(\frac{x-x_{i}}{h_i}\right)-k_ih_i\psi\left(\frac{x_{i+1}-x}{h_i}\right)+k_{i+1}h_i\psi\left(\frac{x-x_{i}}{h_i}\right)$

求二阶导数有

$\begin{aligned} s''_i(x_{i+1})&=6\frac{y_i}{h_i^2}-6\frac{y_{i+1}}{h_i^2}+2\frac{k_i}{h_i}+4\frac{k_{i+1}}{h_i}\\ s''_{i+1}(x_{i+1})&=-6\frac{y_{i+1}}{h_{i+1}^2}+6\frac{y_{i+2}}{h_{i+1}^2}-4\frac{k_{i+1}}{h_{i+1}}-2\frac{k_{i+2}}{h_{i+1}} \end{aligned}$

令 $s''_i(x_{i+1})=s''_{i+1}(x_{i+1})$，有

$\beta_ik_i+\alpha_{i+1}k_{k+1}+\beta_{i+1}k_{i+2}=\eta_i+\eta_{i+1}$

其中 $\beta_i=\frac1h_{i},\ \alpha_{i+1}=2(\beta_{i}+\beta_{i+1}),\ \eta_i=3\frac{y_{i+1}-y_i}{h_i^2}$. 加上额外的约束条件，即可转化为求解一个对角占优的三对角或接近三对角线性方程组。

三次样条插值的好处在于它能最小化势能，其中势能定义为

$E(t)=\|t''(x)\|_2=\int_a^b[t''(x)]^2dx$

有以下结论：

• 令 $s(x)$ 为自然样条，则 $E(s)\le E(g),\ \forall g \in \mathcal W_0=\{g\in C^2[x_0,x_n]:g(x_i)=f(x_i)\}$
• 令 $s(x)$ 为完全样条，则 $E(s)\le E(g),\ \forall g \in \mathcal W_1=\{g\in \mathcal W_0:g'(x_0)=f(x_0),\ g'(x_n)=f(x_n)\}$

可以令 $r(x)=g(x)-s(x)$，那么有

$\int_{x_0}^{x_n}[g''(x)]^2dx=\int_{x_0}^{x_n}[s''(x)]^2dx+\int_{x_0}^{x_n}[r''(x)]^2dx+2\int_{x_0}^{x_n}s''(x)r''(x)dx$

而

$\begin{aligned} \int_{x_0}^{x_n}s''(x)r''(x)dx&=\sum\limits_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}s''(x)r''(x)dx\\ &=\sum\limits_{i=0}^{n-1}\left.s''(x)r'(x)\right|_{x_i}^{x_{i+1}}-\int_{x_i}^{x_{i+1}}s'''(x)r'(x)dx\\ &=s''(x_n)r'(x_n)-s''(x_0)r'(x_0)-s'''(x_n)r(x_n)+s'''(x_0)r(x_0)\\ &\ \ \ \ \ \ \ \ \ +\sum\limits_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}s''''(x)r(x)dx \end{aligned}$

因为 $s(x)$ 为三次函数，所以有 $s''''(x)=0$，$\int_{x_i}^{x_{i+1}}s''''(x)r(x)dx=0$. 同时 $r(x_n)=r(x_0)=0$

对于自然样条，$s''_0(x_0)=s''_{n-1}(x_n)=0$，所以有 $\int_{x_0}^{x_n}s''(x)r''(x)dx=0$;

对于 $g \in \mathcal W_1$，$r'(x_n)=r'(x_0)=0$，所以有 $\int_{x_0}^{x_n}s''(x)r''(x)dx=0$。

于是结论成立。

对于三次样条插值的误差界，有如下结论

$\|s^{(j)}(x)-f^{(j)}(x)\|_\infty\le\|f^{(4)}(x)\|_\infty \cdot O(h^{4-j}),\ j \in \{0,1,2\}$

General Interpolation

---

以上讨论的都是插值函数的基为多项式的情况。本节讨论采用一般的基进行插值时的情况。

此时问题变为：给定 $(x_1,y_1),\dots,(x_n,y_n)\in \R^m \times \R,\ (x_i \neq x_j, \forall i,j)$ 和 $\phi_1(x),\dots,\phi_n(x):\R^m\to \R$，找到一个函数 $\phi(x)\in \text{span}\{\phi_1(x),\dots,\phi_n(x)\}$ 使得 $\phi(x_i)=y_i, \forall i$

同样可以转化为求解线性方程组的问题。只需要设 $\phi(x)=c_1\phi_1(x)+\cdots+c_n\phi_n(x)$，则有

$\begin{bmatrix} \phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_n(x_1)\\ \phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_n(x_2)\\ \vdots & \vdots & \ddots & \vdots\\ \phi_1(x_n) & \phi_2(x_n) & \cdots & \phi_n(x_n) \end{bmatrix} \begin{bmatrix} c_1\\c_2\\ \vdots \\c_{n} \end{bmatrix} = \begin{bmatrix} y_1\\y_2\\ \vdots \\y_n \end{bmatrix}$

对于不同的基，矩阵有不同的形式，需要对特定问题再进行分析，这里就不再展开。

常用的基函数有：多项式、分段多项式、有理函数、三角函数、镜像基函数、小波基函数

Two-Dimensional Interpolation

---

本节讨论二维插值问题。

Lagrange Interpolation

Lagrange 多项式插值对于一些特定的插值点有唯一解，如矩形网格、等距三角形网格。Lagrange 多项式插值并不总是适定的（存在唯一解）。有如下定理：

令 $\mathcal P$ 为二元多项式的有限维向量空间。多项式插值问题在 $\mathcal P$ 中适定当且仅当 $(x_1,y_1),\dots,(x_n,y_n)$ 不在任意一条代数曲线 $p(x,y)=0$ 上。

以下介绍两种二维插值的方法。

Shepard’s Method

Shephard 方法的思想是离插值点越近，受插值点函数值的影响就越大。具体如下：

$F(x,y)=\sum\limits_{i=1}^nz_i\cdot\omega_i(x,y)$

其中 $\omega_i(x,y)$ 为权函数，满足 $\sum\limits_{i=1}^n\omega_i(x,y)=1$.

一个经典权函数为

$\omega_i(x,y)=\frac{\left\|\begin{bmatrix}x-x_i\\y-y_i\end{bmatrix}\right\|^{-p}}{\sum\limits_{j=1}^n\left\|\begin{bmatrix}x-x_j\\y-y_j\end{bmatrix}\right\|^{-p}},\ \ p\ge 1$

$\omega_i(x,y)$ 与距离有关，并且距离越小，权重越大

Delaunay triangulation – dual of Voronoi diagram

Delaunay triangulation 和 Voronoi diagram 的示例如下

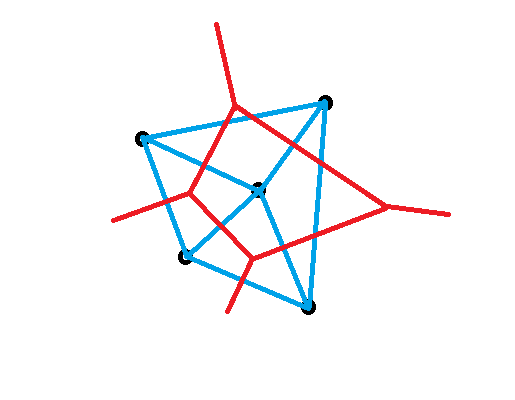
其中黑色点为给定的插值点，蓝色线为Delaunay triangulation，红色为Voronoi diagram，两个互为对偶关系。每一块红色区域内的点都与区域内的插值点最近。通过 Delaunay triangulation 得到的插值方法就是根据估计点最近的三个插值点，即 Delaunay triangulation 的顶点来进行线性插值。具体如下：

假设三个插值点分别为 $A,B,C$，则

$s(x,y)=\alpha f(x_A,y_A)+\beta f(x_B,y_B)+\gamma f(x_C,y_C)$

其中 $(\alpha,\beta,\gamma)$ 为 $(x,y)$ 的重心坐标，可以通过以下方程求解

$\begin{bmatrix} x\\y\\1 \end{bmatrix} = \begin{bmatrix} x_A & x_B & x_C\\ y_A & y_B & y_C\\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} \alpha\\\beta\\\gamma \end{bmatrix}$